11 Plus Verbal Reasoning
Type L - Alphabet Series/Sequence
With this type of question you are required to work out the sequence (or sequences) of pairs of letters that are shown and to complete the series by filling in the blanks.
It is important that your child understands the concept of sequences before attempting this. Work through Number Sequences and Patterns first.
The actual test questions involve pairs of letters, but it is best to begin with single letters and to become familiar with the different types of relationships that can make up the sequences.
You are normally given an Alphabet Line to assist with these type of questions,
but ensure that your child can write one from memory.
A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
Look at this example: Find the next letter in the series - A C E G I K
As with numbers, a useful strategy for dealing with sequences is to write them down, giving enough space to draw and label the hops from one term to another.
By using the alphabet and counting from one letter to the next you can see that the sequence is moving forwards through the alphabet, 2 letters at a time. Mark these steps as a series of hops until you are certain of the rule. In this case, count forward in twos. When you reach the last letter, K, continue the pattern, + 2, which gives M.

Lets look at another example: Find the next letter in the series - X U R O L I
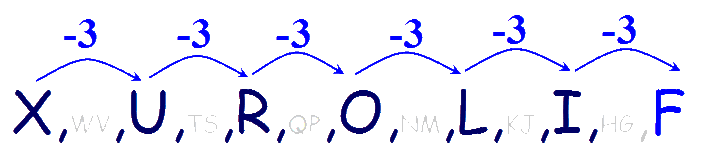
By using the alphabet and counting from one letter to the next you can see that the sequence is moving backwards through the alphabet, 3 letters at a time. Mark these steps as a series of hops until you are certain of the rule. In this case, count backwards in three's. When you reach the last letter, I, continue the pattern, -3, which gives F.
There can be many variations of this type of question. The key to solving these is to write down and label the relationships between the letters - this will highlight the rule. Make sure that you check that the rule is correct for the whole series - it is very easy to think that you have the rule after 1 or 2 hops, only to find that the rule is more complex than it looks!
More examples of different sequences: |


