Subtracting Fractions
Subtraction is the inverse of addition, so the same rules apply to subtracting as adding.
To subtract like fractions (same denominator) you just subtract the numerators and keep the denominator the same.
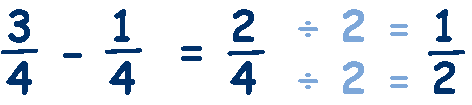
If you look carefully, you will see that we have subtracted the numerators, 3 - 1 = 2, but the denominator has remained the same, 4, and then simplified by dividing the numerator and denominator by 2 to give ½. Lets try another:
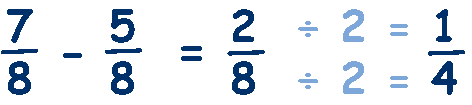
We have subtracted the numerators, 7 - 5 = 2, but the denominator has remained the same, 8, and then simplified by dividing the numerator and denominator by 2 to give ¼
To subtract fractions that have different denominators, we have to change the fractions so that the denominators are the same - change them into like fractions.
Look at this example: 
The only way we can subtract these fractions is if the denominators are the same - so lets change the thirds into sixths. To make the denominator a 6 we multiply it by 2, because
3 x 2 = 6, and remember that we must do the same to the top and bottom. So we also multiply 2 x 2 = 4. Changing the fraction from 2/3 to 4/6.

Now both fractions have the same denominator so we can simply subtract the numerators.

Lets try a more difficult example, say, 
The problem we now have is that the denominators are not the same and we cannot change one denominator into the other easily. The solution is to find a denominator that is common to both numbers - a common denominator. The easiest way to find a common denominator is to multiply the denominators, ie 6 x 5 = 30,
Now we change both fractions so that their denominators are 30.
(basically we multiply each fraction by the other fractions denominator).
 and and 
Now both fractions have the same denominator so we can simply subtract the numerators.
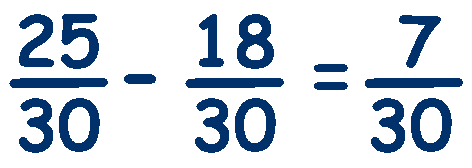
|
