Calculating with Fractions
Before we begin calculating with fractions, lets refresh some terms.
A Proper Fraction is when the numerator is smaller than the denominator.
An Improper Fraction is when the numerator is greater than the denominator.
A Mixed Number is a mixture of whole numbers and fractions.
and add a new term.
If two or more fractions have the same denominator, they are known as 'Like Fractions'.
so 1/4 and 3/4 are like fractions, as are 3/25, 9/25, 23/25 etc
A Like Fraction has the same denominator (bottom number).
Adding Fractions
Think about adding two like fractions, say, one quarter plus one quarter, you probably know that the answer is two quarters because you can easily imagine having two quarters of a cake and putting them together - you have two quarters or one half.
But how can we write a calculation for this?

If you look carefully, you will see that we have added the numerators, 1 + 1 = 2, but the denominator has remained the same, 4. Lets try another:
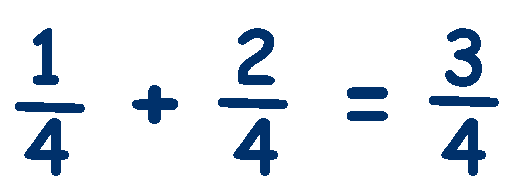
We have added the numerators again, 1 + 2 = 3, and the denominator has again remained the same, 4.
To add like fractions (same denominator) you just add the numerators and keep the denominator the same.
Now think about adding two fractions that have different denominators, say, one quarter plus one eighth, you cant really visualise this and get a precise answer because they are different quantities - quarters and eighths.
The only way we can add these fractions is if the denominators are the same - so lets change the quarter into eighths. To make the denominator an 8 we multiply it by 2 because 4 x 2 = 8, and remember that we must do the same to the top and bottom. So we also multiply 1 x 2 = 2. Changing the fraction from 1/4 to 2/8.
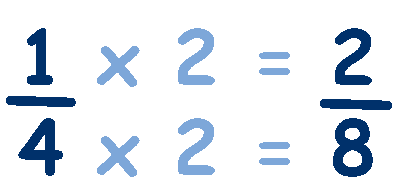
Now both fractions have the same denominator so we can simply add the numerators.

Lets try a more difficult example, say one half plus one third, 
The problem we now have is that the denominators are not the same and we cannot change one denominator into the other easily. The solution is to find a denominator that is common to both numbers - a common denominator. The easiest way to find a common denominator is to multiply the denominators, ie 2 x 3 = 6,
Now we change both fractions so that their denominators are 6.
(basically we multiply each fraction by the other fractions denominator).
 and and 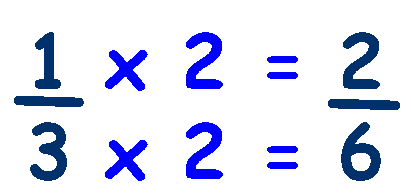
Both fractions now have the same denominator so we can add the numerators.

|
