Algebra - Rearranging Equations
Sometimes an equation will have letters and numbers on both sides of the equals sign .... 6y + 2 = 5y + 7
We need to rearrange this equations so that all the letters are on one side of the equals sign and all the numbers are on the other side - so that all the letters are grouped together and all the numbers are grouped together.
This is the second rule to remember:
'Letters on one side and numbers on the other'
How do we do this? - First decide which side of the equals sign you are going to have the letters - look at the equation, there is '6y' on the left and '5y' on the right - try to make sure that the side with the largest value is the side you keep the letters on.
So in this case we will keep the letters on the left.
Look at the left side first, 6y + 2, to only have letters on this side we need to remove the number 2 or take it away (-2) We have used the 'inverse' to remove it (inverse of '+' is '-')
This is the third rule to remember:
'Use the inverse operation'
this gives us 6y +2 -2 which leaves 6y on the left.
The equation is now unbalanced though 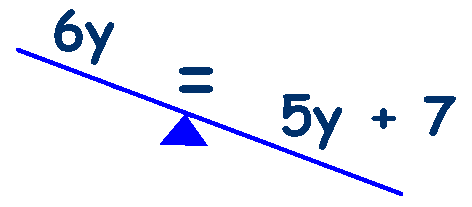
Remember the 1st rule -
'Do the same to both sides to keep the equation balanced'
So we now need to do the same, -2, to the right side, 5y + 7 - 2, or 5y + 5
The equation is now balanced again 
We now have to remove the letters from the right side, 5y + 5, remove 5y
or take it away (-5y) by using the inverse.
'Use the inverse operation'
this gives us 5y - 5y + 5 which leaves 5 on the right.
The equation is now unbalanced again 
'Do the same to both sides to keep the equation balanced'
So we now need to do the same, -5y, to the right side, 6y - 5y, which leaves 'y'
The equation is now balanced again 
We took the same away from both sides and the equation remained balanced
and in the process we discovered that y = 5
Check your result by putting your answer into the original equation
6y + 2 = 5y + 7 is 6 x 5 + 2 = 5 x 5 + 7 is 32 = 32 ✔
(dont forget to do the multiplying first)
Work through this slowly, step by step and repeat the rules each time that you use them.
'Do the same to both sides to keep the equation balanced'
'Letters on one side and numbers on the other'
'Use the inverse operation'
With these three rules you can solve any Algebra problem.
This Equation Machine from 'Maths is Fun' is excellent for visualising the process.
______________________________________________________
Jump to:
Equations Balancing Equations Rearranging Equations Examples Order of Operations |
